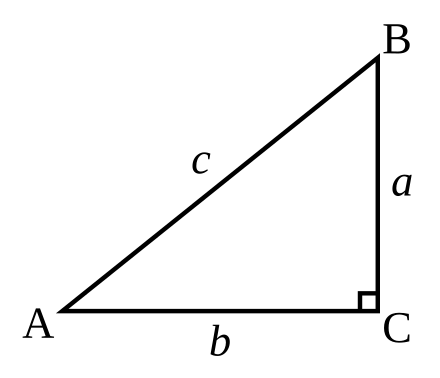
Generate Pythagorean Triples using an identity You'll gain access to interventions, extensions, task implementation guides, and more for this instructional video In this lesson you will learn to generate a Pythagorean Triple by using the identity (x^2 y^2)^2 (2xy)^2 = (x^2 y^2)^2The problem above requires us to do two things First, generate a Pythagorean Triple using the integers 3 and 5Second, we need to figure out if the generated triple is Primitive or ImprimitiveFind an answer to your question find the identity of x^2y^2 =?

How To Use The Pythagorean Theorem With A Circle Veritas Prep
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples-👍 Correct answer to the question The identity (x^2y^2)^2 = (x^2y^2)^2 (2xy)^2 can be used to generate pythagorean triples what pythagorean triple could be generated using x=8 and y=3 ehomeworkhelpercomThe Pythagorean triple Identity is (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2, where c = x 2 y 2, a = x 2 y 2, and b = 2xy With x = 3 and y = 5 a = 3 2 5 2 = 16, (this is 16, by the rules x should be greater than y (x > y), in this case √(x 2 y 2) 2 = a) b = 2*3*5 = 30 c = 3 2 5 2




Answered Example 3 Jeremy Uses The Polynomial Bartleby
X and y are positive integers;Use the Pythagorean identity, (x^2y^2) (2xy)^2 = (x^2y^2)^2 , to create a Pythagorean triple Follow these steps 1 Choose two numbers and identify which is replacing x and which is replacing y 2 How did you know which number to use for x and for y?👍 Correct answer to the question Use the identity (x^2y^2)^2=(x^2−y^2)^2(2xy)^2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6 eeduanswerscom
The identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean The identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3?Correct answers 2 question The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triplePlease help Thanks in advance We have x2=2xy 3y2 = 0 Are there supposed to be 2 equal signs in this expression or is it x2 2xy 3y2 = 0 ?
HSAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triplesX2 y2 can be written as (xy)2 this is in the form of (a b)2 = a2 2ab b2so the above can be written as x2 2xy y2or there is another one too x2 y2 =For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, the
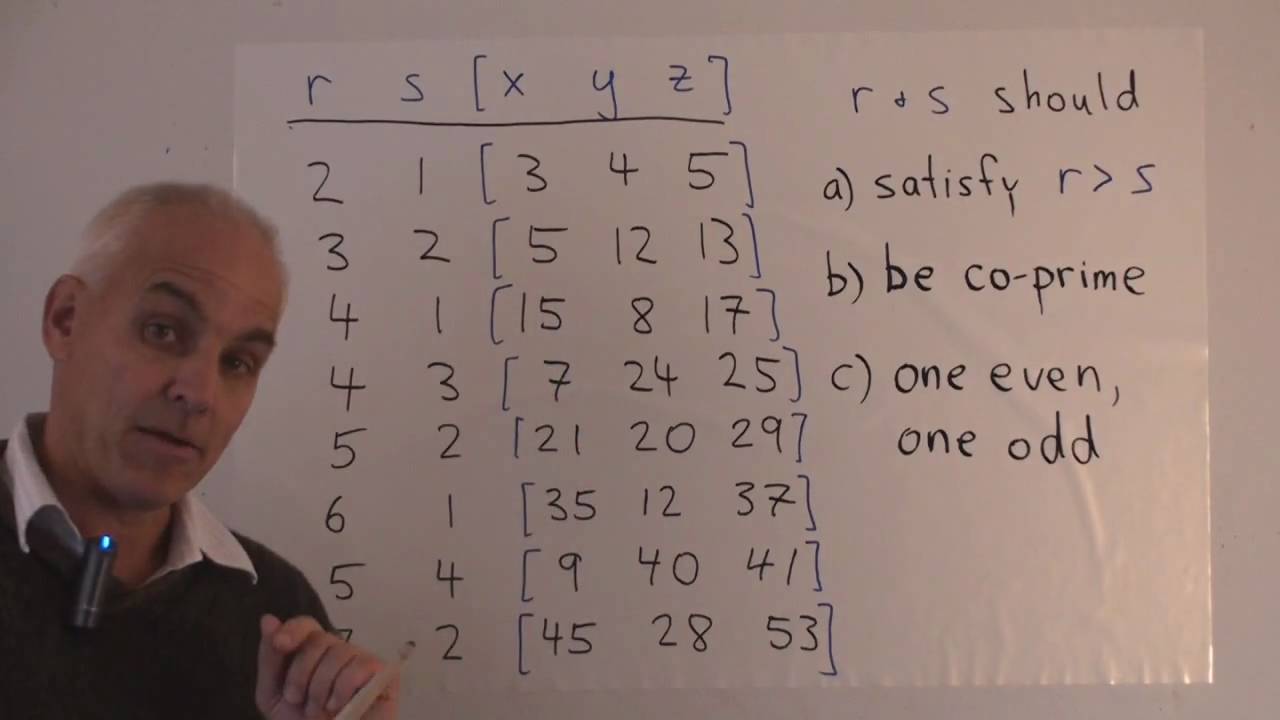



Pythagorean Triples Explanation Examples




The Modular Tree Of Pythagoras Citeseerx
Example 2 Use the integers 3 and 5 to generate a Pythagorean Triple Is the generated triple a Primitive or Imprimitive Pythagorean Triple? Correction (after missing a sign) As kobe pointed out, the original DE is $$ (x^2y^2)y'2xy=0, $$ which as equation for a vector field reads $$ (x^2y^2)\,dy2xy\,dx=0\iff Im(\bar z^2\,dz)=0\text{ with } z=xiy $$ From the complex interpretation it is directly visible that this is not integrable, for that it would have to be an expression Saikiran Reddy and Kwasi F give excellent solutions to this The answer, dy/dx =1 might make us think about the question a bit For x^2y^2=2xy, we get (by differentiating implicitly), dy/dx =1 That's the same as the derivative of a linear function with slope, 1 Hmmmmm Let's see If we have x^2y^2=2xy The we must also have x^22xy y^2=0 Factoring gets us (xy)^2




Use The Pythagorean Identity X2 Y 2 2xy 2 X2 Y2 2 To Create A Pythagorean Brainly Com



Www Mcpsmt Org Cms Lib Mt Centricity Domain 3501 Precalc textbook stewart Pdf
Satyajeetdamekar004 satyajeetdamekar004 Math Secondary School answeredStudents will prove the polynomial identity ( x^2 y^2 )^2 ( 2xy )^2 = ( x^2 y^2 )^2 and use it to generate Pythagorean triplesUse this activity as independent/partner practice or implement it as guided notes and practice for students in need ofCCSSMathContentHSAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Authors National Governors Association Center for Best Practices, Council of Chief State School Officers




The Identity X2 Y22 X2 Y22 2xy2 Can Be Used To Gen Gauthmath



Q Tbn And9gcsq3z2c4nz5yt7lp57 Tx6pv0yyscku6wrvxorjn3fjot7w8yo Usqp Cau
Use the identity (x^2y^2)^2=(x^2−y^2)^2(2xy)^2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6Further remarks May 6 The polynomial ring $\mathbb{H}u$ has a natural division ring of fractions, $\mathbb{H}(u)$, which is isomorphic to a certain ring of $2 \times 2$ matrices over $\mathbb{C}(u)$ (I can't get the latex right for matrices, but the ring should be clear in particular, the determinants of elements in the ring are elements of $\mathbb{R}(u)$)Find dy/dx x^2y^2=2xy Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate Tap for more steps By the Sum Rule, the derivative of with respect to is Differentiate using the Power Rule which states that is where




900 Algebra 2 Ideas Algebra 2 Algebra Lesson Plans



Http Www Math Northwestern Edu Mlerma Problem Solving Putnam Training Problems 13 Pdf
Marshall uses the polynomial identity (x?y)^2=x^2?2xyy^2 to show that 8 = 64 What values can Marshall use for x and y?Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity $(x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2$ can be used to generate Pythagorean triplesSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Recognize Patterns That Make Pythagorean Triples Learnzillion



Www Jstor Org Stable
Determine the dimensions of the squares that must be cut to create a box with Calculus The line that is normal to the curve x^2=2xy3y^2=0 at(1,1) intersects the curve at what other point? Answer 2 📌📌📌 question The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3?Correct answers 2 🔴 question Type the correct answer in each box In part E, you proved that any Pythagorean triple can be generated using the identity (x^2 − y^2)^2 (2xy)^2 = (x^2 y^2)^2 Find the missing x and yvalues and Pythagorean triples using the identity given Write the triple in parentheses, without spaces between the values, with a comma between values, and in order




How To Use The Pythagorean Theorem With A Circle Veritas Prep




Polynomial Identities Solutions Examples Videos Worksheets Games Activities
Answer 2 📌📌📌 question The identity (x^2y^2)^2 = (x^2y^2)^2 (2xy)^2 can be used to generate pythagorean triples what pythagorean triple could be generated using x=8 and y=3 the answers to estudyassistantcom3 Explain how to find a Pythagorean triple using those numbers 4Use the Pythagorean identity, Latex (x^2y^2)^2(2xy)^2=(x^2y^2)^2\textsf{,} to create a Pythagorean triple Follow these steps Choose two numbers and identify which is replacing




Generate Pythagorean Triples Using An Identity Learnzillion




Type The Correct Answer In Each Box In Part E You Proved That Any Pythagorean Triple Can Be Brainly Com
Theorem The positive primitive solutions of x^2 y^2 = z^2 with y even are x = r^2 s^2, y = 2rs, z = r^2 s^2, where r and s are arbitrary integers of opposite parity with r>s>0 and gcd(r,s)=1 Using this theorem, find all solutions of the equation x^2 y^2 = 2z^2 (hint write theCalculus Find two numbers whose sum is 10 for which the sum of their squares is a minimum algebra The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;Add − x 2 y 2 x 2 y 2 and x 2 y 2 x 2 y 2 Add x 2 x 2 x 2 x 2 and 0 0 Simplify each term Tap for more steps Multiply x 2 x 2 by x 2 x 2 by adding the exponents Tap for more steps Use the power rule a m a n = a m n a m a n = a m n to combine exponents Add 2 2 and 2 2



Www Degruyter Com Document Doi 10 1515 Math 17 0111 Pdf



Http Alpha Math Uga Edu Pete 4400full Pdf
HSAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2 ) 2 = (x 2 y 2 ) 2 (2xy) 2 can be used to generate Pythagorean triplesExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music The identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y



How To Find Pythagorean Triplets With One Given Number Quora



Pythagorean Theorem And Its Many Proofs
4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples With the increase in technology and this huge new thing called the Internet, identity theft has become a worldwide problem If `x=1&y=3` then prove the identity `(xy)^2=x^22xyy^2` If `x=1&y=3` then prove the identity `(xy)^2=x^22xyy^2` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Biology NCERT NCERT Exemplar NCERTUse the identity (x2y2)2=(x2?y2)2(2xy)2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6




Curiousmathsknols Mathematics For The Curious Page 2




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download
Correct answers 2 question Use the identity (x^2y^2)^2=(x^2−y^2)^2(2xy)^2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6The answers to estudyassistantcom👍 Correct answer to the question Use the identity (x^2y^2)^2=(x^2−y^2)^2(2xy)^2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6 ehomeworkhelperscom



2




Pythagoras Matrix Mathematics Determinant
Consider x^ {2}y^ {2}xy22xy as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and m divides the constant factor y^ {2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factorAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples




U X 2 Y 2 2xy U X 2 Y 2 2xy U X 1 2 Chegg Com




Understanding Pythagorean Identities Studypug




Pdf Pythagorean Triples Before And After Pythagoras Ravi Agarwal Academia Edu




Pdf Pythagorean Triples Before And After Pythagoras



Http Www Math Brown Edu Jhs Frintdir Frintch2ch3 Pdf




Answered Example 3 Jeremy Uses The Polynomial Bartleby




Heron S Formula Descartes Circles And Pythagorean Arxiv Math v1 Math Mg 22 Jan Pdf Document



Times Module M15 Pythagoras Theorem



Pythagorean Triangles And Triples




Understanding Pythagorean Identities Studypug



Pythagorean Triples



Http M Hikari Com Ijma Ijma 14 Ijma 33 36 14 Catarinoijma33 36 14 Pdf




Pythagorean Triples Video Lessons Examples Step By Step Solutions



3



Hal Archives Ouvertes Fr Hal Document



Pythagorean Theorem And Its Many Proofs




Calameo Precalculo Schaum




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download




Pythagorean Triplet In An Array Geeksforgeeks




Analyzing Polynomial Identities Video Khan Academy



Diophantine Equation Wikiwand



Www Jstor Org Stable 10 4169 College Math J 48 2 115




004 Sum Sums Of Three Squares A Collection Of Algebraic Identities




Unit 6 A Pythagoras Sides Of Squares Trainer Instructor Notes Pythagoras Sides Of Squares Geometry Pdf Document




900 Algebra 2 Ideas Algebra 2 Algebra Lesson Plans




Pythagorean Triple From Wolfram Mathworld



Pythagorean Triples Before And After Pythagoras Document Gale Academic Onefile



Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions



Www Cjoint Com Doc 02 Jbkwanbk3vv Article2 Pdf




If X 3 A N D Y 1 Find The Values Of Each Of The Using Identi



Pythagorean Triangles And Triples



Pythagorean Triples Generator Youtube



2



Www Brewtoncityschools Org Cms Lib Al Centricity Domain 133 8 2 The Pythagorean Theorem And Its Converse Pdf




Answered Show That X Y X Y Bartleby



Pythagorean Triples Additive Problems And More Springerlink




Pythagorean Theorem How To Use Pythagoras Theorem With Examples




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Math Questions Math Answers



Www Cjoint Com Doc 02 Jbkwanbk3vv Article2 Pdf




Mathematics 2 Demo Scope And Sequence And 4 Sample Units By Grupo Anaya S A Issuu




Pdf Pythagorean Triples Before And After Pythagoras



1



Pythagorean Identities Mathbitsnotebook Ccss Math




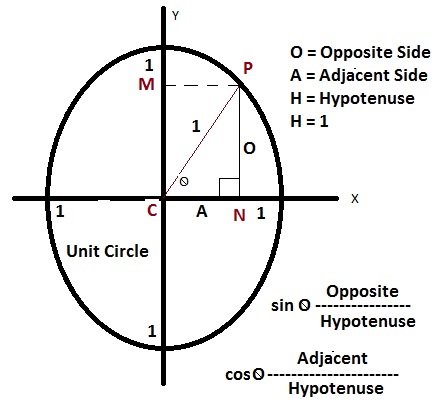
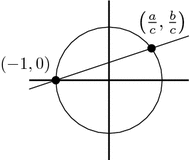
Generating Pythagorean Triples Chilimath




6 The Abc S Of Number Theory



Solving Pythagorean Identities Trigonometry Calculator




Lesson 10 The Power Of Algebra Finding
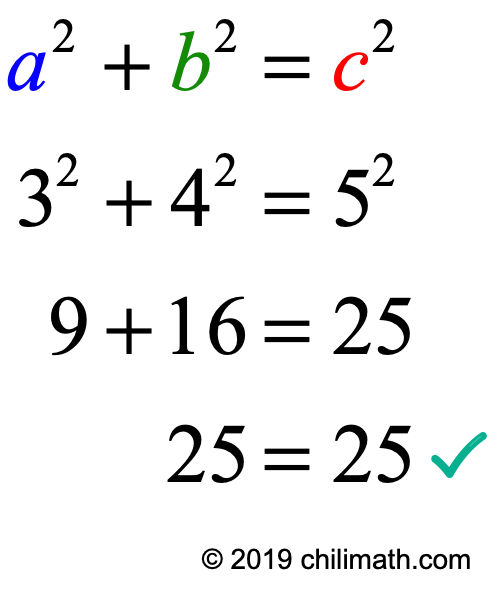



Generating Pythagorean Triples Chilimath




Mathgaz01 More Properties Of Pythagorean Triples Elementary Mathematics Number Theory



Elearning Reb Rw Course View Php Id 277




Generating Pythagorean Triples 360




Pythagorean Theorem An Overview Sciencedirect Topics



Times Module M15 Pythagoras Theorem




The Academy Corner Dong Thap In South Vietnam Portal Manualzz




Pythagorean Triple From Wolfram Mathworld



Pythagorean Triangles And Triples



Http Www Math Odu Edu Jhh Geometry Pdf



What Is A Nice Way To Construct Pythagorean Triplets Quora




Pdf Postprint Of Some Relations Among Pythagorean Triples




Pythagorean Theorem Wikipedia




M Sc Maths Thesis Pradeep Mishra



The Double Continuity Of Algebra Springerlink



2




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Pythagorean Triples




Pythagorean Triples Keith Conrad Pdf Free Download
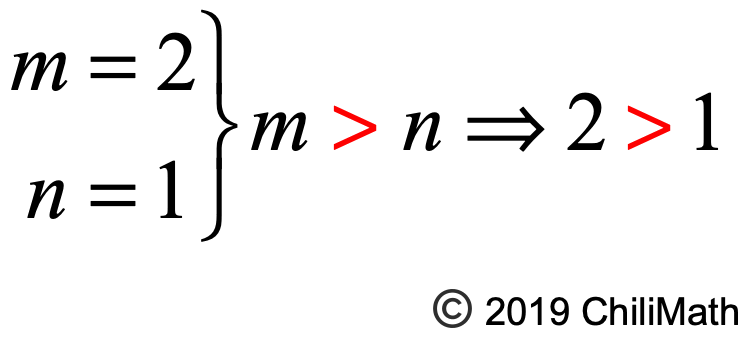



Generating Pythagorean Triples Chilimath



The Identity X2 Y22 X2 Y22 2xy2 Can Be Used To Gen Gauthmath




Curiousmathsknols Mathematics For The Curious Page 2
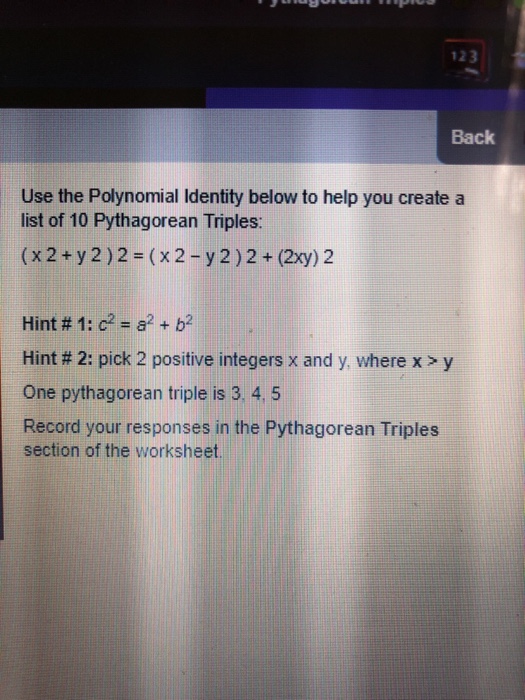



123 Back Use The Polynomial Identity Below To Help Chegg Com




Pythagorean Theorem How To Use Pythagoras Theorem With Examples




Formulas For Generating Pythagorean Triples Wikipedia



2




A Apr 4 Objective Adding Amp Subtracting Polynomials Prove Polynomial Identities And Use Them




Pythagorean Theorem An Overview Sciencedirect Topics




Pythagorean Triples Keith Conrad Pdf Free Download
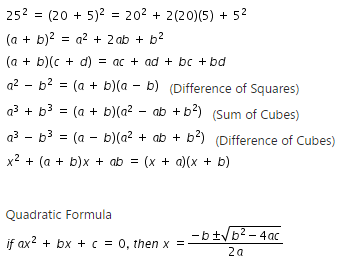



Mafs 912 A Apr 3 4 Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example The Polynomial Identity X Y X Y 2xy Can Be Used To Generate Pythagorean Triples



How To Find Pythagorean Triplets With One Given Number Quora




Pythagorean Triple Worksheets Teaching Resources Tpt



3



Www Maths Ed Ac Uk V1ranick Papers Hatchertn Pdf


